The given differential equation is(3x 4y 1)dx (4x 5y 1)dy = 0 (i)Comparing Eq (i) with Mdx Ndy = 0, we get M = 3x 4y 1and N = 4x 5y 1Here, ∂M∂y = ∂N∂x = 4Hence, Eq (i) is exact and solution is given by ∫3x 4y 1dx ∫5y 1dy = C⇒ 3x22 4xy x 5y22 y C = 0⇒ 3x2 8xy 2x 5y2 2y 2C = 0⇒ 3x2 2 4 xy 2x 5y2 2y C = 0where, C10 Find the order and degree of the differential equation dx2 6/5 dy dx 6 8 Evaluate Evaluate Evaluate sin4 x cos6 x 3 4 5 to the Circle x' 2gx 2fy c = O Find the angle between the circles x2 — 12x — 6y 41 = O and x 2 y 2 4x6y —59=0 Find the equation of the parabola whose focus is S(I, 7) and vertex is A(I, 2) Show that the curves 2x^23y^2=5 and y^2=x^3 are orthogonal at (1,1) and (1,1) Use parametric mode to draw the curves math Two circles of radius 4 are tangent to the graph of y^2=4x at the point (1,2) Find the equation of these two
How To Show That Y Mx Is A Tangent Of The Circle X Y 2gx 2fy C 0 If G Mf C 1 M Quora
X^2+y^2+2gx+2fy+c=0 differential equation
X^2+y^2+2gx+2fy+c=0 differential equation-General Equation of the Second Degree The equation of the form is a x 2 2 h x y b y 2 2 g x 2 f y c = 0 When a, b and h are not simultaneously zero, is called the general equation of the second degree or the quadratic equation in x and y Homogeneous Equation An equation of the form f ( x, y) = 0 is said to be the homogeneous equation of degree n, where n is a positiveFind slope of the CP




Engineering Mathematics Notes
If the circle x^2y^22gx2fyc=0 bisects the circumference of the circle x^2y^22g^(prime)x2f^(prime)yc^(prime)=0 then prove that 2g^(prime)(gg^(prime))2f^(prime)(ff^(prime))=cc ' Updated On 246\ \Rightarrow b y^2 2fy a x^2 2gx 2C = 0\ The above equation represents a circle \\text{ Therefore, the coffecients of }x^2\text{ and }y^2\text{ must be equal These are respectively y = m x c, ( x − h) 2 ( y − k) 2 = r 2, y = ( a x b) c x d, a x 2 2 h x y b y 2 2 f x 2 g y 1 = 0 The geometric conditions are euclidean motion, curvature, curvature variations The number of geometric conditions equals number of arbitrary geometric constants or differentiations to arrive at an
The given equation isx 2 y 2 2gx2fyc=0 (1)Differentiating once with respect to x, we get2x2yy'2g2fy'=0 (2)Differentiating again, we get22yy''2 (y') 2 2fy''=0or, 1yy'' (y') 2 fy''=0 (3)Differentiating once again, we gety'y''yy'''2y'y''fy'''=0or, yy'''3y'y''fy'''=0 (4)Substituting the value of f from equation (2) in equation (4), we get the required differentialAx^22hxyby^22gx2fy c =0, actually represents the general equation of any second degree curve(the second order conics like circle,parabola,ellipse,hyperbola and rectangular hyperbola) So, by putting h=0 we get ax^2by^22gx2fyc= 0 which does represent a circle with centre at(g,f) and radius=sqrt(g^2f^2c) The general equation of a circle is x 2 y 2gx 2fy c = 0 (i) Since it passes through origin (0, 0), it will satisfy equation (i) ⇒ 2(0)2 (0) 2g(0) 2f(0) c = 0 ⇒ c = 0 ⇒ 2 2x y 2gx 2fy = 0 This is the equation of a circle
Then the equation of parabola is given by (y – β) 2 = 4a (x – α) which is equivalent to x = Ay 2 By C If three points are given we can find A, B and C Similarly, when the axis is parallel to the y – axis, the equation of parabola is y = A'x 2 B'x C' Illustration Find the equation of the parabola whose focus is (3 , 40 votes 1 answerSubtract y^ {2} from both sides Subtract y 2 from both sides 2gx2fyc=0\sin (\frac {\mathrm {d}} {\mathrm {d}x} (y))\cos (\pi x)x^ {2}y^ {2} 2 g x 2 f y c = 0 s i n ( d x d ( y)) c o s ( π x) − x 2 − y 2 Subtract 2gx from both sides Subtract 2 g x from both sides



2




Complex Number
If the equation `x^2y^22h x y2gx2fyc=0` represents a circle, then the condition for that circle to pass through three quadrants only but not pass asked in Mathematics by JohnAgrawal (910k points) class12;The parametric equation of the circle x2 y2 2gx 2fy c = 0 is x = g rcosθ, y = f rsinθ Here, θ is a parameter, which represents the angle made by the line, joining the point (x, y) with the center, with the X axis That's it for this lesson See you in the next one! If L = l x m y n = 0 is tangent to circle x 2 y 2 2 g x 2 f y c = 0 then find point of contact I know that equation of tangent is S 1 = x x 1 y y 1 g ( x x 1) f ( y y 1) c = 0 anf rearranging I obtain S 1 = ( g x 1) x ( f y 1) y g x 1 f y 1 c = 0 By comparing coefficients it should give the point of contact



2




If The Two Circle X 2 Y 2 2gx C 0 And X 2 Y 2 2fy C Have Equal Radius Askiitians
Key Point The general equation of a circle is x 2y 2gx2fy c = 0, where the centre is given by (−g,−f) and the radius by r = p g2 f2 − c The equation can be recognised because it is given by a quadratic expression in both x and y with no xy term,Answer (1 of 6) The equation x^2y^22gx2fyc=0 comes from the definition of the circle itself The definition of circle is "All the points that are equidistant from a single point" & tge distance is the radius of the circle Consider a circle with radius 'r' & let its center be located at (gThe general equation of conics of a second degree is given by \(a{x^2} 2hxy b{y^2} 2gx 2fy c = 0\) and discriminant Δ = abc 2fgh – af 2 – bg 2 – ch 2 The above given equation represents a nondegenerate conics whose nature is given below in the table




What Is The Radius Of A Circle With The Equation X2 Y2 2gx 2fy C 0 Quora




Engineering Mathematics Notes
If P(x, y) be a variable point on the parabola then PS = PM in the figure and this yields the equation to the parabola 2 2 (hx ky)2 hk2 h2 k = x− 2 y− 2 , h2 k2 h k2 h k2 On simplification, the above equation reads y x 2 y x − 1 = 0, −2 k h k h or more compactly, x y ± ± = 1, h and k being parameters h k CarryingLet C_1x^2y^22gx2fyc=0 and C_2=x^2y^22gx2fyc_1=0 Now note that C_1=(xg)^2(yf)^2=f^2g^2c and C_2=(xg)^2(yf)^2=f^2g^2c_1 Now assuming that c\ge c_1, C_1 is contained inSolution For The differential equation which represents the three parameter family of circlesx2y22gx2fyc=0 is The differential equation which represents the three parameter fam Filo About Us Become a Tutor Blog Download App




The Order Of The Differential Equation Whose Solution Is X 2 Y 2 2gx 2fy C 0 Is




Page 3 Differential Geometry High Resolution Stock Photography And Images Alamy
Equation of Tangent to a Circle A tangent to a circle is a straight line which intersects (touches) the circle inexactly one point Let the equation of the circle be x 2 y 2 2gx 2fy c = 0 Let P(x 1, y 1) be a given point on it Let PT be the tangent at P The centre of the circle is C(− g, − f) How To Derive?To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If the straight lines `ax^2 2hxy by^2 2gx 2fy c = 0` intersect on the XThe General Form of the equation of a circle is x 2 y 2 2gx 2fy c = 0 The centre of the circle is (g, f) and the radius is \(\rm \sqrt{g^2f^2c}\)




A Circle X 2 Y 2 2gx 2fy C 0 Passes Through Three Co Normal Points On The Par Youtube




Answered 2 E V Ycos Xy Dx 2xe2y Xy Bartleby
The GS is y^2 = (A x^4)/(2x^2) Or, alternatively y = sqrt(A x^4)/(sqrt(2)x) We have (x^2 y^2) \\ dx xy \\ dy = 0 Which we can write in standard form as dy/dx = (x^2 y^2)/(xy) 1 Which is a nonseparable First Order Ordinary Differential Equation A suggestive substitution would be to perform a substitution of the form y = xv => dy/dx = v xv' \\ \\ \\ whereFirst order differential equation (dy dx)4 (dy dx)2 − 5x = 0 The maximum derivative of y with respect to x is dy dx Second order differential equation d2y dx2 7y = 0 The maximum derivative of y with respect to x is d2y dx2 Third order differential equation∎ If S ≣ x 2 y 2 2gx 2fy c = 0 and S' ≣ x 2 y 2 2g'x 2f'y c' = 0 are two intersecting circles, then S λS' = 0, λ ≠ −1 , is the equation of the family of circles passing through the points of intersection of S = 0 and S' = 0 ∎ If S ≣ x 2 y 2 2gx 2fy c = 0 is a circle which is intersected by the straight line μ ≣ ax by c = 0 at two




Scheme Of Studies



Page 3 Differential Geometry High Resolution Stock Photography And Images Alamy
If the equation `ax^(2)2hxyby^(2)2gx2fyc=0` jointly represents two lines whose separation equations are `xy=0` and `2x3y=1` then `g=` asked 2 days ago in Straight Lines by Somyek (The general equation of a circle is given by x 2 y 2 2gx 2fy c = 0 We will discuss some of the ways of finding the family of circles under the given certain conditions Let S = x 2 y 2 2gx 2fy c = 0 S 1 = x 2 y 2 2g 1 x 2f 1 y c 1 = 0 S 2 = x 2 y 2 2g 2 x 2f 2 y c 2 = 0 L = lx my n = 0 1 Family of2hxy 2gx 2fy c = 0, the origin is to be shifted to the point In this case, the transformed equation is 2hXY c = 0 7 The xy term is removed from ax 2 2hxy by 2 2gx 2fy c = 0 by rotation of axes through an angle θ = 8The condition that the equation ax 2 2hxy by 2 2gx 2fy c = 0,




If The Equation Of The Circle Obtained Byreflecting The Circle X 2 Y 2 A 2 0 In The Liney Mx C Is X 2 Y 2 2gx 2fy C 0 Then A G Frac 2mc 1 M 2 C A 2 B G Frac 2mc 1 M 2 F Frac 2c 1 M 2 C G Frac 2mc 1 M 2 Frac 4c 2




Ppt Circle Equations Powerpoint Presentation Free Download Id
For the differential equation d x d y 1 x 3 3 x 2 y = 1 x 3 sin 2 x The solution is y ( 1 x 3 ) = A 1 x − B 1 sin 2 x c , where c is the constant of integration, then find B/A?Find eqn to the cone with vertex at origin and base is x2y2 = 4 and z=2 (this is a guiding curve, circle lies on the xy plane) Try this same as example (5) 7 Find eqn to the cone with vertex at (0,0,0) which passes through the curve of intersection of x2 y2z2 x 2y 3z 4 = 0 and xyz=2 Try this also Homogenize these two eqnsWhere g , f & c are arbitary constants



2



Page 3 Analytical Geometry High Resolution Stock Photography And Images Alamy
The general solution of the differential equation of all circles having centre at A( 1, 2) is x 2 y 2 2x 4y c = 0 Explanation General equation of a circle with centre ( g, f) is x 2 y 2 2gx 2fy c = 0 If ( g, f) = A ( 1, 2) Then equation of circle, x 2 y 2 2x 4y c = 0Let the equation of the circle be x 2 y 2 2gx 2fy c = 0 If it passes through (0, 0), then c = 0 The equation of circle is x 2 y 2 2gx 2fy = 0 Since the centre of the circle lies on y–axis then g = 0 The equation of the circle is x 2 y 2 2fy = 0(i) This represents family of circles Dertermine the equation with center (h,k) Example 2 Find the center and the radius of the circle x 2 y 2 5x6y5=0 Comparing with the general equation, x 2 y 2 2gx2fyc=0 g=5/2 f=3 c=5 Hence,the center is (5/2,3) and the radius is 14



Link Springer Com



Kea Kar Nic In
Obtain the differential equation of the family of circles x^2 y^2 2gx 2fy c = 0 ;The Order Of The Differential Equation Whose Solution Is X 2 Y 2 2gx 2fy C 0 Is The order of the differential equation whose solution is x 2 y 2 2gx 2fy c = 0 is 1) 1The line x = y touches a circle at the point (1, 1) If the circle also passes through the point (1, 3), then its radius is




Obtain The Differential Equation Of The Family Ofcircles X 2 Y 2 2gx 2fy C 0 Where G F C Are Arbitrary Constants Snapsolve




Ppt Mathematics Powerpoint Presentation Free Download Id
JEE Main & Advanced Mathematics Differential Equations Question Bank Order and degree of differential equations question_answer The order of the differential equation whose solution is \{{x}^{2}}{{y}^{2}}2gx2fyc=0\, is MP PET 1995Example 4 The order of the differential equation whose solution is x2 y2 2gx 2fy c 0, is (a) 1 (b) 2 (c) 3 (d) 4 Solution (c) To eliminate the arbitrary constants g, f and c, we need 3 more equations, that by differentiating the equation 3 times Hence highest order derivative will be 3 3 dx d yChapter 42 FIRST ORDER DIFFERENTIAL EQUATION 5 Hrs Solution of first order variable separable type differential equation Simple Problems Chapter 43 LINEAR TYPE DIFFERENTIAL EQUATION 4 Hrs x 2 y 2gx 2fy c = 0 –––––– (2) Add g 2, f on both sides




Circles
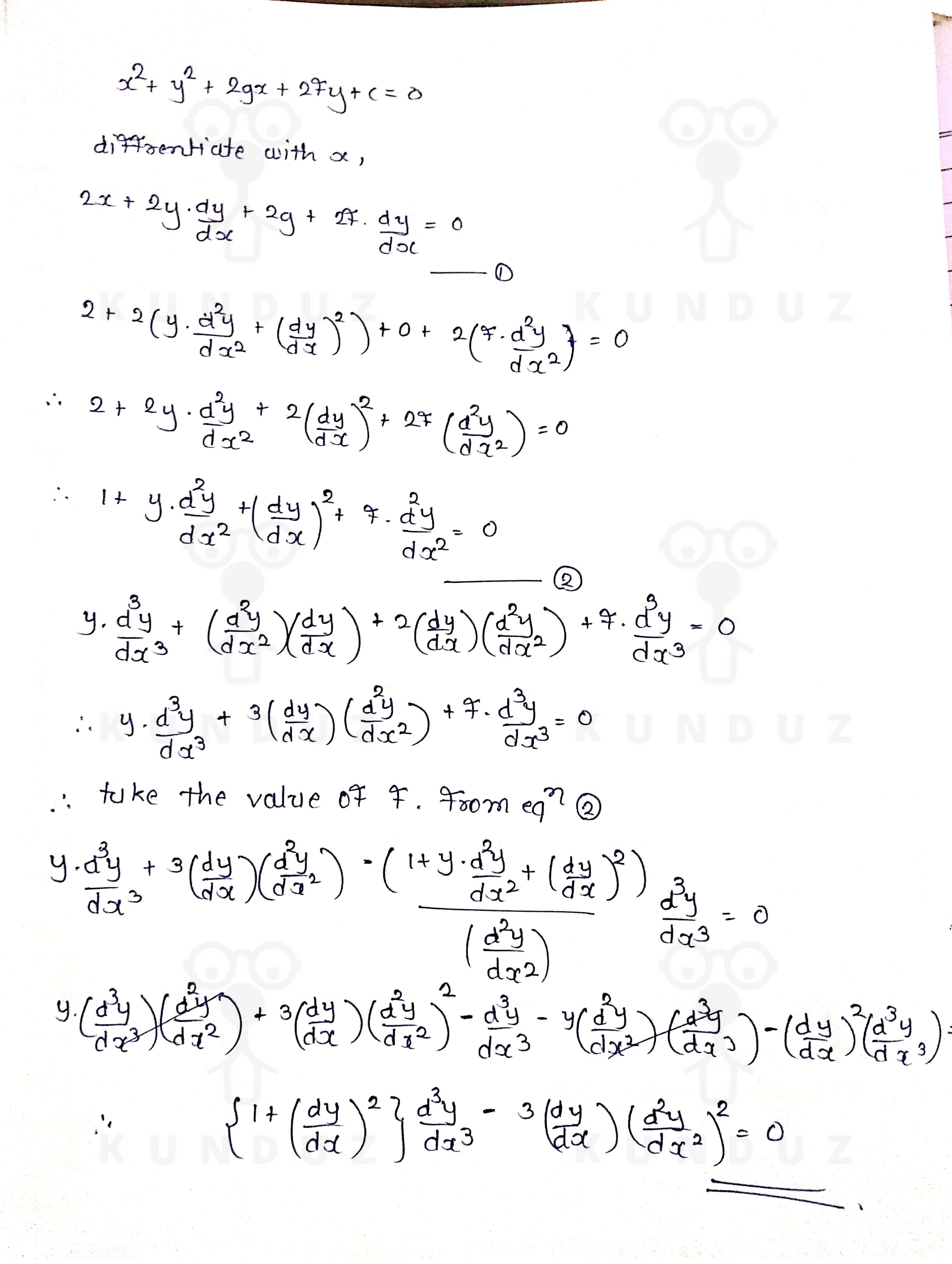



Show That The Differential Equation Of The Family Of Ci Math
We know that the equation of circle with centre (g, f) and radius √g 2 f 2c is x 2 y 2 2gx 2fy c =0 So, the equation of concentric circle is x 2 y 2 2gx 2fy c' = 0 Here we observe that both the equations have the same centre, but have different radii and c ≠ c' Similarly, a circle with centre (h, k), and the radius r, will have the equation ( x – h ) 2 ( y – k )The order of the differential equation whose solution is \{{x}^{2}}{{y}^{2}}2gx2fyc=0\, is MP PET 1995A collection of circles is called as a system or family of circles There can be various types of family of circles The general equation of a circle is x2 y2 2gx 2fy c = 0 Since this equation involves three unknowns ie g, f and c so we need at least three conditions to get a unique circle




Math1 1




The Equation Ax 2 By 2 2hxy 2gx 2fy C 0 Represents A Circle Only If
The equation of any conic can be expressed as ax^2 2hxy by^2 2gx 2fy c = 0 ax2 2hxy by2 2gx2f y c = 0 However, the condition for the equation to represent a circle is a = b a = b and h = 0 h = 0 Then the general equation of the circle becomes x^2 y^2 2gx 2fy c = 0 x2 y2 2gx 2f yc = 0Here is the equation of the concentric circle – x 2 y 2 2gx 2fy c = 0 is x 2 y 2 2gx 2fy k = 0 (Equation differs only by the constant term) 2 Contact of Circles When the outer surfaces of two circles are touching, it is known as contact of circles There may be two cases in contact with circles




The Solution Of X 1 X 2 Dx Y 1 Y 2 Dy 0 Is



How To Show That Y Mx Is A Tangent Of The Circle X Y 2gx 2fy C 0 If G Mf C 1 M Quora
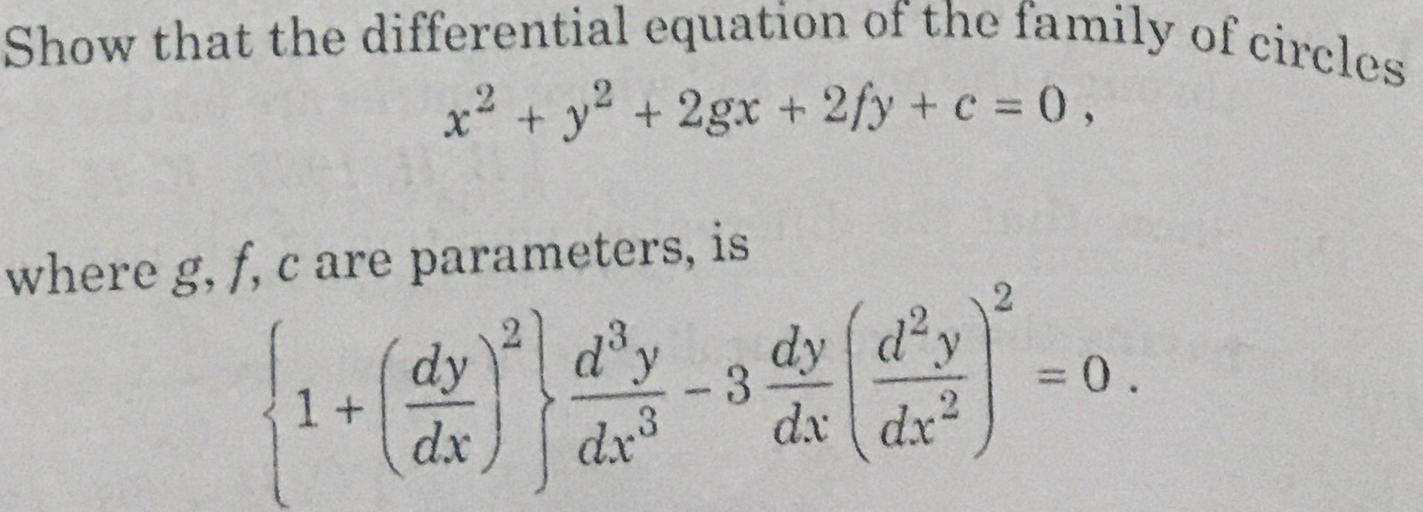



Show That The Differential Equation Of The Family Of Ci Math
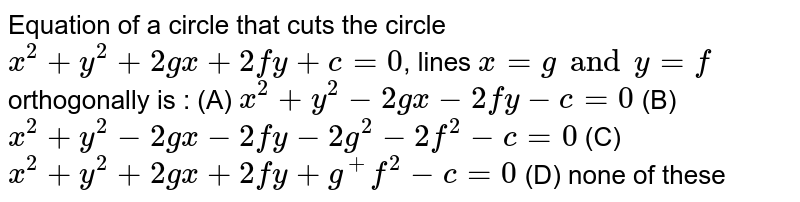



Equation Of A Circle That Cuts The Circle X 2 Y 2 2gx 2fy C 0 Lines X G And Y F Orthogonally Is A X 2 Y 2 2gx
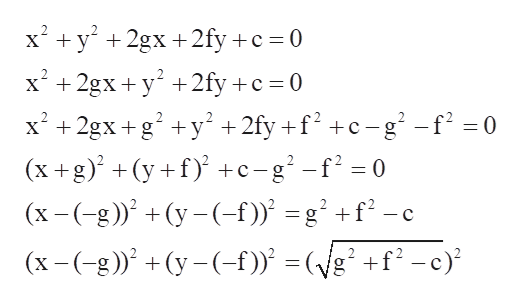



Answered I D Like To Know How To Find Center Of Bartleby
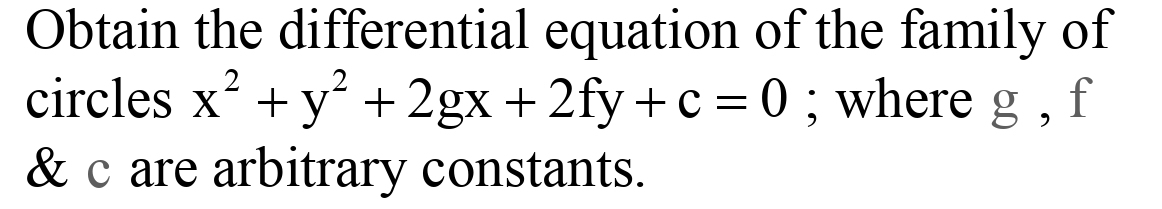



Obtain The Differential Equation Of The Family Ofcircles X 2 Y 2 2gx 2fy C 0 Where G F C Are Arbitrary Constants Snapsolve



L The Distance Between The Chords Of Contact Oftangents To The Circle X 2 Y 2 2gx 2fy C 0from The Origin And From The Point G F Is1 Sqrt G 2 F 2 2 Frac Sqrt G 2 F 2 C 2 3 Frac G 2 F 2 C 2sqrt G 2 F 2 4 Frac




Mathematics Notes



Aimstutorial In
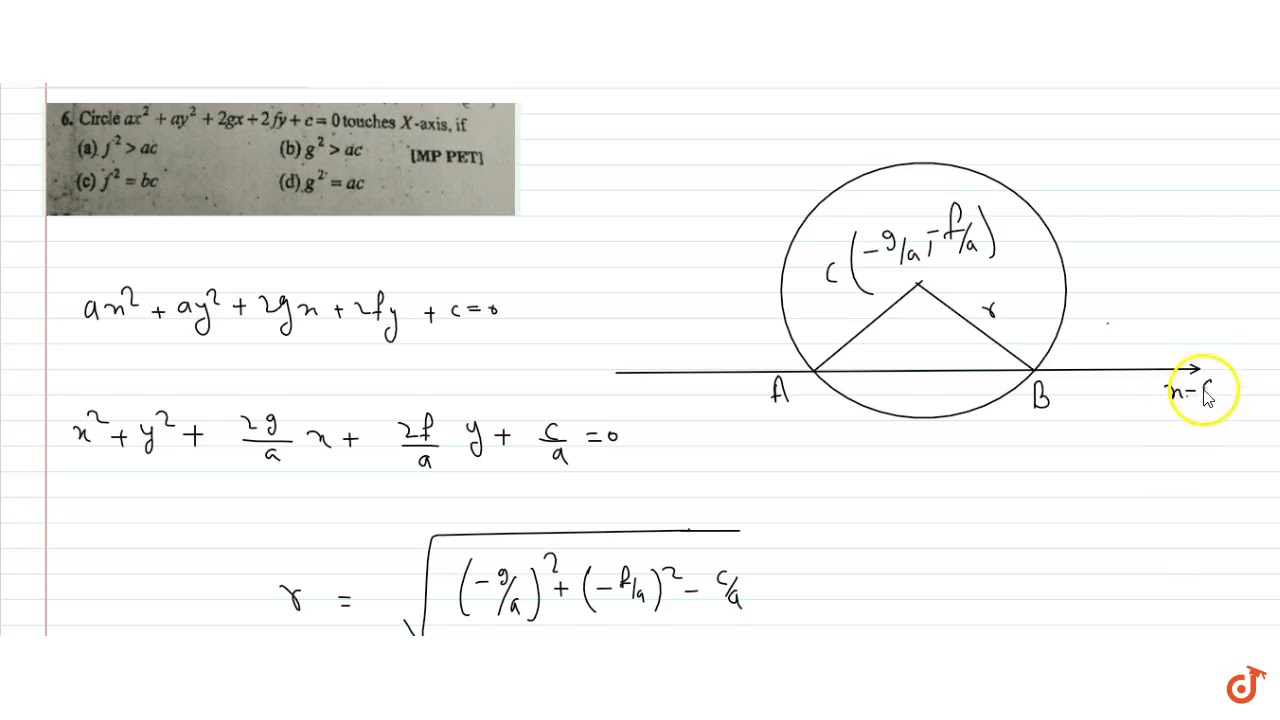



Circle Ax 2 Ay 2 2gx 2fy C 0 Touches X Axis If Youtube



Jstor Org



2




The Circle X 2 Y 2 2gx 2fy C 0 Does Not Intersect X A Xi S If G 2 Ltc B G 2 Gt C Youtube



Selfstudys Com




The Centre Of Variable Circle X 2 Y 2 2gx 2fy C 0 Lies On The Line 2x 2y 9 0 An Youtube



What Are All The Conditions For The General Equation Of Pair Of Straight Lines To Represent A Pair Of Straight Lines Quora



Why The Equation Of Circle Is X 2 Y 2 2gx 2fy C 0 Where Did This Equation Came From Quora




Show That The Differential Equation Of The Family Of Ci Math




Mathematics Notes




Answered Find The Center And Radius Of The Bartleby




Ppt Mathematics Powerpoint Presentation Free Download Id




Ppt Circle Equations Powerpoint Presentation Free Download Id
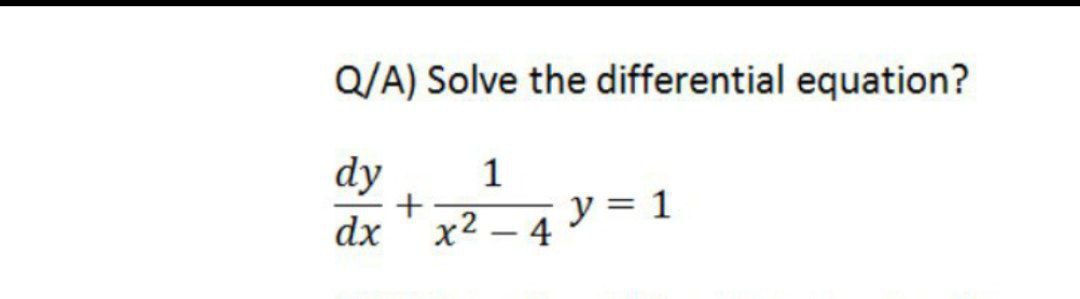



Answered Q A Solve The Differential Equation Bartleby




Circles




If Ax 2 2hxy By 2 2gx 2fy C 0 Then Show That Dy Dx Dx Dy 1 Youtube




The Order Of The Differential Equation Whose Solution Is X 2 Y 2 2gx 2fy C 0 Is
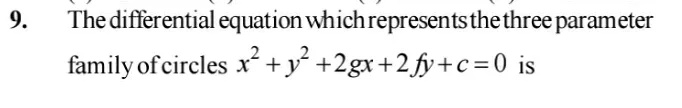



9 The Differential Equation Whichrepresents The Three Parameterfamily Ofcircles X 2 Y 2 2gx 2fy C 0 Is Snapsolve




Circles



Em I Differential Calculus




How To Find An Equation Of 2 Lines From A Pair Of Straight Lines Quora




Ordinary And Partial Differential Eqns M D Raisinghania



Why The Equation Of Circle Is X 2 Y 2 2gx 2fy C 0 Where Did This Equation Came From Quora




Where A Bare Arbitrary Constants Obtain The Differential Equation Of The Family Of Circles X Y 2gx 2fy C 0 Where G Care Arbitrary Constants Obtain The Differential Equation Associated With




Mathsgee Math Solver




Answered Find The Ordinary Differential Equation Bartleby
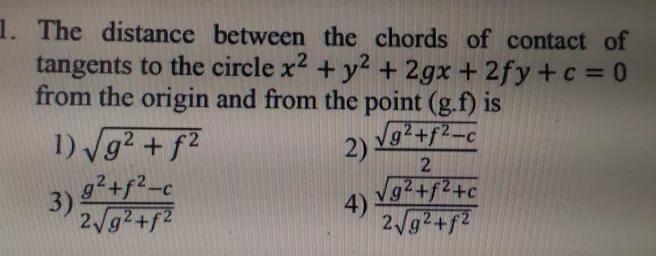



L The Distance Between The Chords Of Contact Oftangents To The Circle X 2 Y 2 2gx 2fy C 0from The Origin And From The Point G F Is1 Sqrt G 2 F 2 2 Frac Sqrt G 2 F 2 C 2 3 Frac G 2 F 2 C 2sqrt G 2 F 2 4 Frac




If Ax2 2hxy By2 2gx 2fy C 0 Find Dy Dx Brainly In




Free Math Help And Resourses Home Facebook



Find The Orthogonal Trajectories Of The Circles X 2 Y 2 Ay 0 Where A Is A Parameter Sarthaks Econnect Largest Online Education Community




Mathematics Notes
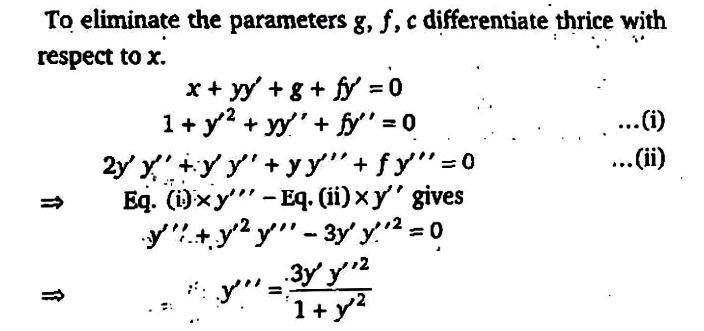



9 The Differential Equation Whichrepresents The Three Parameterfamily Ofcircles X 2 Y 2 2gx 2fy C 0 Is Snapsolve




Obtain The Differential Equation Of The Family Of Circles X 2 Y 2 2gx 2fy C 0 Where G F And C Are Arbitrary Constants
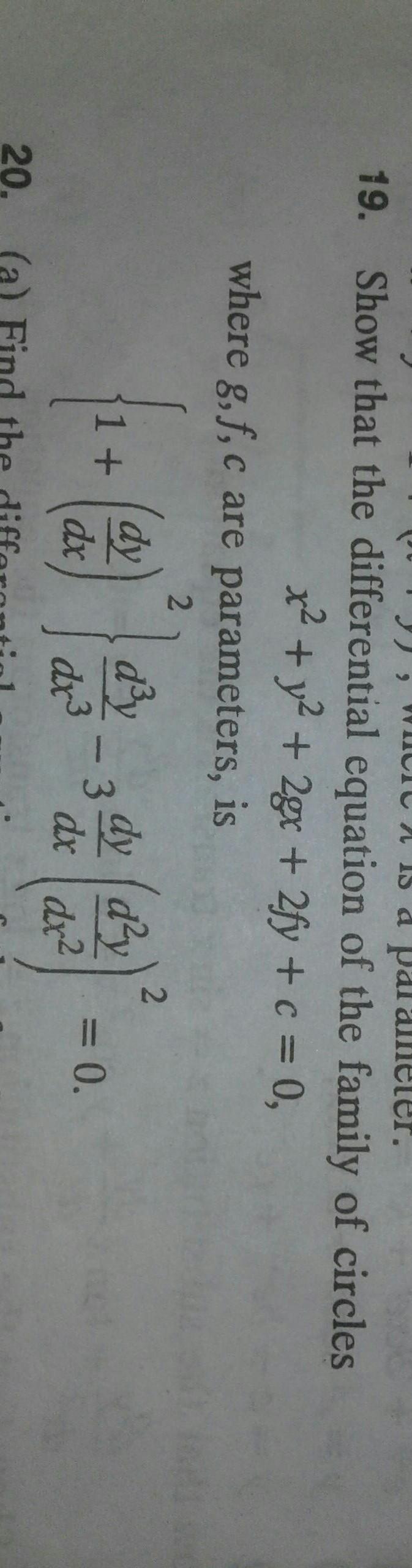



Jv Wc Is A Paralleler 19 Show That The Differenti Math




If The Equation Of The Circle Obtained Byreflecting The Circle X 2 Y 2 A 2 0 In The Liney Mx C Is X 2 Y 2 2gx 2fy C 0 Then A G Frac 2mc 1 M 2 C A 2 B G Frac 2mc 1 M 2 F Frac 2c 1 M 2 C G Frac 2mc 1 M 2 Frac 4c 2




Form The Differential Equation Representing The Family Of Curves Y Mx Where M Is Arbitrary Constant



How To Show That Y Mx Is A Tangent Of The Circle X Y 2gx 2fy C 0 If G Mf C 1 M Quora



Assignmentexpert Com




Solution Parabola And General Equation Of Conic Study Guide Studypool




Circles




Circles




Circles




Circles Pdf Circle Analytic Geometry



Market Edugorilla Com




Possible Areas Or Units Of Selection Of Questions Examination Of Karnataka India




The Differential Equation Of The Family Of Circles Passing Through The Origin And Having Centres On The X Axis Is



When Second Degree Equation Represents A Circle Parts Video Dailymotion




Second Degree Equation Pdf Manifold Teaching Mathematics




Http Www Aplustopper Com Pair Straight Lines Straight Lines Lines Straight



If The Two Circles X 2 Y 2 2gx C 0 And X 2 Y 2 2fy C 0 Have Equal Radius Then Locus Of Youtube



2




Ppt Mathematics Powerpoint Presentation Free Download Id



Mathematics
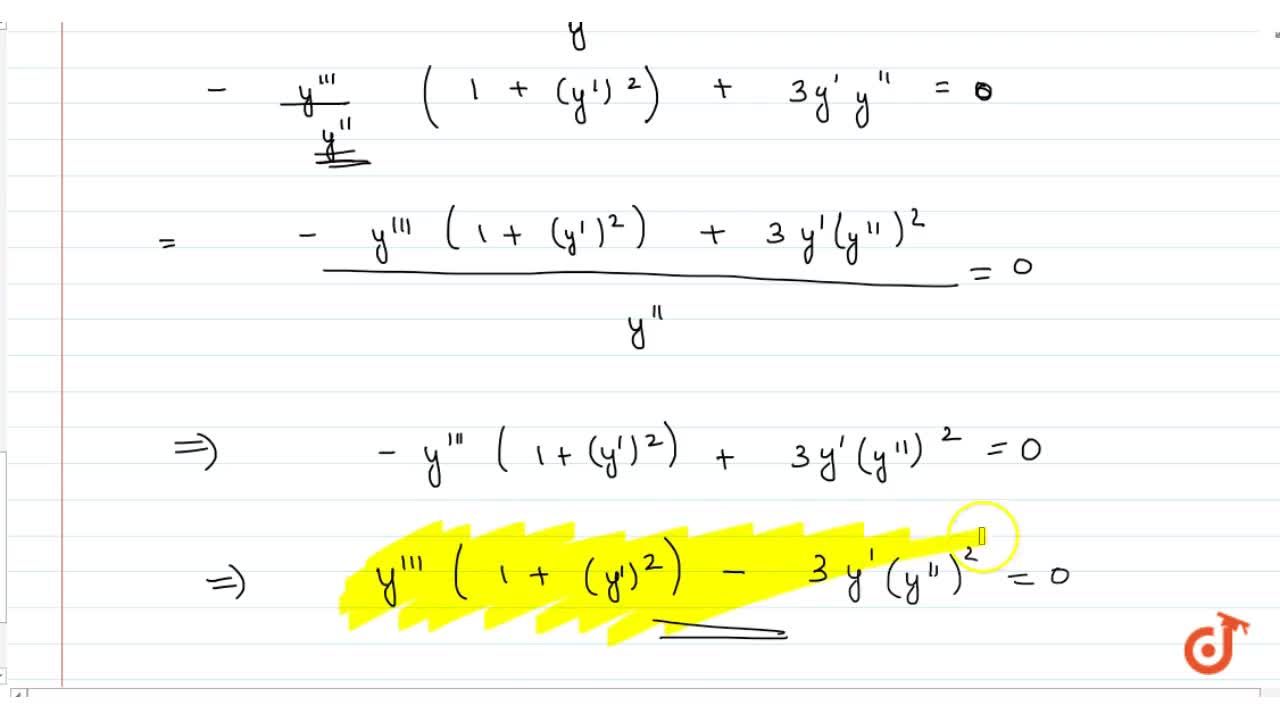



Obtain The Differential Equation Of The Family Of Circles X 2 Y 2 2gx 2fy C 0 Where G F C Are Arbitrary Constants



2



Page 3 Analytical Geometry High Resolution Stock Photography And Images Alamy




Circles



Page 3 Analytical Geometry High Resolution Stock Photography And Images Alamy



Show That The General Equation Of The Second Degree Ax 2 2hxy By 2 2gx 2fy C 0 Sarthaks Econnect Largest Online Education Community




Find The Area Of Equilateral Triangle Inscribed In A Circle X 2 Y 2 2gx 2fy C 0 Youtube




Form The Differential Equation Representing The Family Of Curves Y Mx Where M Is Arbitrary Constant



Why The Equation Of Circle Is X 2 Y 2 2gx 2fy C 0 Where Did This Equation Came From Quora




The Length Of A Tangent Drawn From Any Point On The Circle X Y 2gx 2fy P 0 To The Circle Brainly In




Cptr 5 Class 2 Pdf Circle Euclidean Geometry



Jstor Org




Statement 1 A Body May Gain Kinetic Energy And Potential Energy Simultaneously Andstatement 2 Conservation Of Mechanical Energy May Not Be Valid Every Time



Jee Mathematics Circle And Conic Section Mcqs Set B Multiple Choice Questions For Circles



0 件のコメント:
コメントを投稿